排序算法
冒泡排序
数组中有 n 个数,比较每相邻两个数,如果前者大于后者,就把两个数交换位置;这样一来,第一轮就可以选出一个最大的数放在最后面;那么经过 n-1(数组的 length - 1) 轮,就完成了所有数的排序。元素项向上移动至正确的顺序,就像气泡升至表面一样,冒泡因此而得名。复杂度为O(2^n)
我们想下这个情况,当原数组是,arr = [1,2,4,3];在经过第一轮冒泡排序之后,数组就变成了arr = [1,2,3,4];
此时,数组已经排序完成了,但是按上面的代码来看,数组还会继续排序,所以我们加一个标志位,如果某次循环完后,没有任何两数进行交换,就将标志位 设置为 true,表示排序完成,这样我们就可以减少不必要的排序,提高性能。
最终实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| function bubbleSort(arr) {
var len = arr.length,
temp,
done;
for (var outer = 0; outer < len-1; outer++) {
done = true;
for (var inner = 0; inner < len - 1 - outer; inner++) {
if (arr[inner] > arr[inner+1]) {
temp = arr[inner];
arr[inner] = arr[inner+1];
arr[inner+1] = temp;
done = false;
}
}
if (done) {
break;
}
}
}
|
选择排序
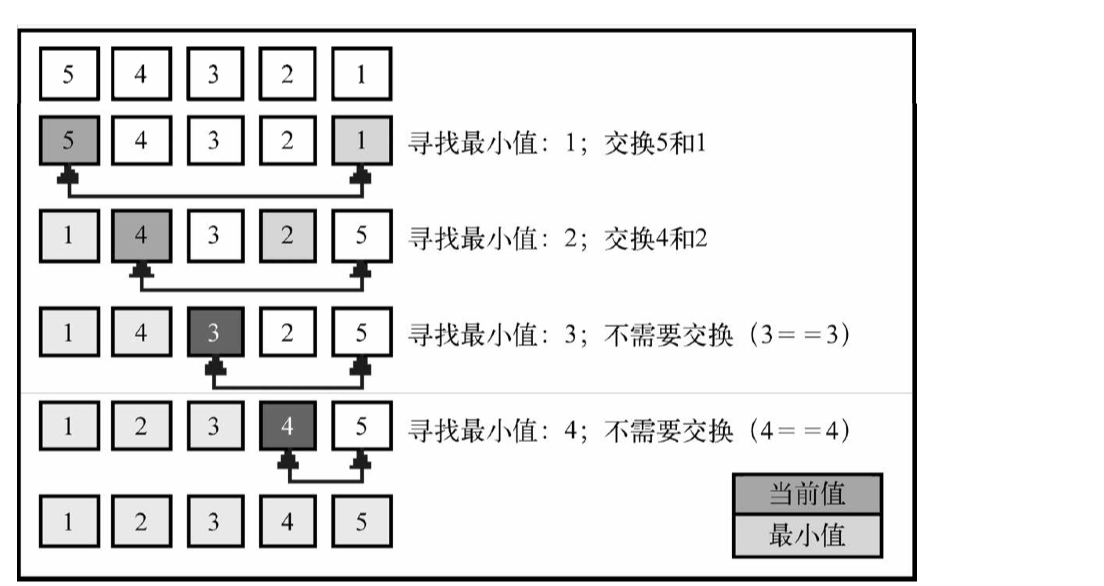
选择排序是一种原址比较排序算法。选择排序的大致思路就是找到数据结构中的最小值并将其放置在第一位,接着找到第二小的值,并将其放在第二位,以此类推。复杂度为O(2^n)
最终实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| function selectionSort(arr) {
var len = arr.length,
indexMin,
temp;
for (var outer = 0; outer < len - 1; outer++) {
indexMin = outer;
for (var inner = outer+1; inner < len; inner++) {
if (arr[indexMin] > arr[inner]) {
indexMin = inner;
}
}
if (indexMin !== outer) {
temp = arr[outer];
arr[outer] = arr[indexMin];
arr[indexMin] = temp;
}
}
}
|
插入排序
选择排序时在两个空间进行,等于说每次从旧的空间选出最值放到新的空间,而插入排序则是在同一空间进行。
可以这么理解,在一个数组中我们不知道哪个是最小值,那么就假定第一个就是最小值,然后取第二个值与第一个值比较产排序后的序列,然后再取第三个值与排序后的序列进行比较插入到对应的位置,依次类推。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| function insertionSort(arr) {
var len = arr.length,
j, temp;
for (var i = 1; i < len; i++) {
j = i;
temp = arr[i];
while(j>0 && arr[j-1] > temp) {
arr[j] = arr[j-1];
j--;
}
arr[j] = temp;
}
}
|
归并排序
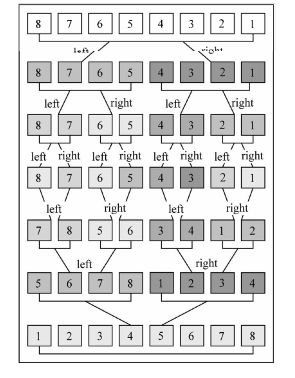
归并排序是一种分治算法。其思想是将原数组切分成较小的数组,直到每个小数组只有一个位置,接着小数组归并成较大的数组,直到最后只有一个排序完毕的大数组。

最终实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| function mergeSort(array) {
return mergeSortRec(array);
};
var mergeSortRec = function(array) {
var length = array.length;
if (length === 1) {
return array;
}
var mid = Math.floor(length / 2),
left = array.slice(0, mid),
right = array.slice(mid, length);
return merge(mergeSortRec(left), mergeSortRec(right));
}
var merge = function(left, right) {
var result = [],
il = 0;
ir = 0;
while(il < left.length && ir < right.length) {
if (left[il] < right[ir]) {
result.push(left[il++]);
} else {
result.push(right[ir++])
}
}
while(il < left.length) {
result.push(left[il++]);
}
while(ir < right.left) {
result.push(right[ir++])
}
return result;
}
console.log(mergeSort([8,7,6,5,4,3,2,1]))
|
快速排序
搜索算法
顺序搜索
二分搜索


